报告Covid-19疫情爆发中中国确诊所需时间的延迟和变化
本文还未经过同行评审。分析内容将会根据最新数据进行更新。
翻译人: Hongyu (Vivian) Liu
目的
确定在疫情爆发过程中传染力(再生数)的变化.
主要结果:
- 随着时间的推移,确诊单例病例的延迟已减少到大约五天。
- 在现在这个时间点,没有证据表明COVID-19在中国的传播已经放缓。
- 估计COVID-19的基本传染数在早期流行爆发期为:2.0-3.8(95%置信区间)。
局限性:
- 根据估计尚未确诊的疑似病例数量以增加近期病例数量是不准确的,这取决于当前观察到的确诊单例病例时间的延迟是否可以代表整个疫情爆发期。
- 近期再生数的上升可能是因为确诊单例病例的过程时间更快了,但我们的评估并未能相应更新。
- 报告使用了来自中国各地的数据,但中国不同地区的病毒传播能力和医疗诊断能力可能有所不懂,这为报告结果增加了不确定性。
- 报告中所使用的方法总体对于无法及时报告案例的情况是有力的,但是会受到报告案例占所有案例比例的影响;比如近期媒体的关注可能导致了寻求医疗帮助方式的变化,这会使得我们的估计不再准确。
方法:
为了降低删失偏差,我们对中国发布的确诊病例数进行了校准,即将为了将会出现的潜在病例进行了估算。我们通过使用经验分布函数分析确了诊花费的时间。数据来源于公共领域报道中的汇编案例集。我们从真实病例合集中(包括估算出而尚未确诊的病例)根据负二项分布随机抽取病例,其中每个病例有pi的独立概率被确诊,i是报告截止日期前症状持续的天数,pi是第i个病例有症状后第i天被确诊的累积分布函数。
我们使用更正后的病例数和EpiEstim R软件包预测了每天的基本传染数,结合了连续病例间隔分布和观察到的病例数量。我们将时间窗设为两天,对估算值进行了光滑处理。我们对连续病例间隔分布的三种情况进行了测试:根据早期流行病传播原理模拟,平均再生数为7.5天,标准差为3.4天;根据类似SARS传播原理模拟,平均再生数为8.4天,标准差为3.8天;根据类似MERS传播原理模拟,平均再生数为6.8天,标准差为4.1天。
结果:
确诊延迟时间
从出现症状到确诊的平均延迟时间为5.6天。有迹象表明,这种延迟会随着时间的推移而下降。特别是在国家卫生与健康委员会特别工作组访问武汉后,确认案例可能会激增,这些病例可能已有症状很长时间。因此,在进一步分析中,我们仅使用2020年1月21日之后发现症状的病例,平均延迟时间为5天。
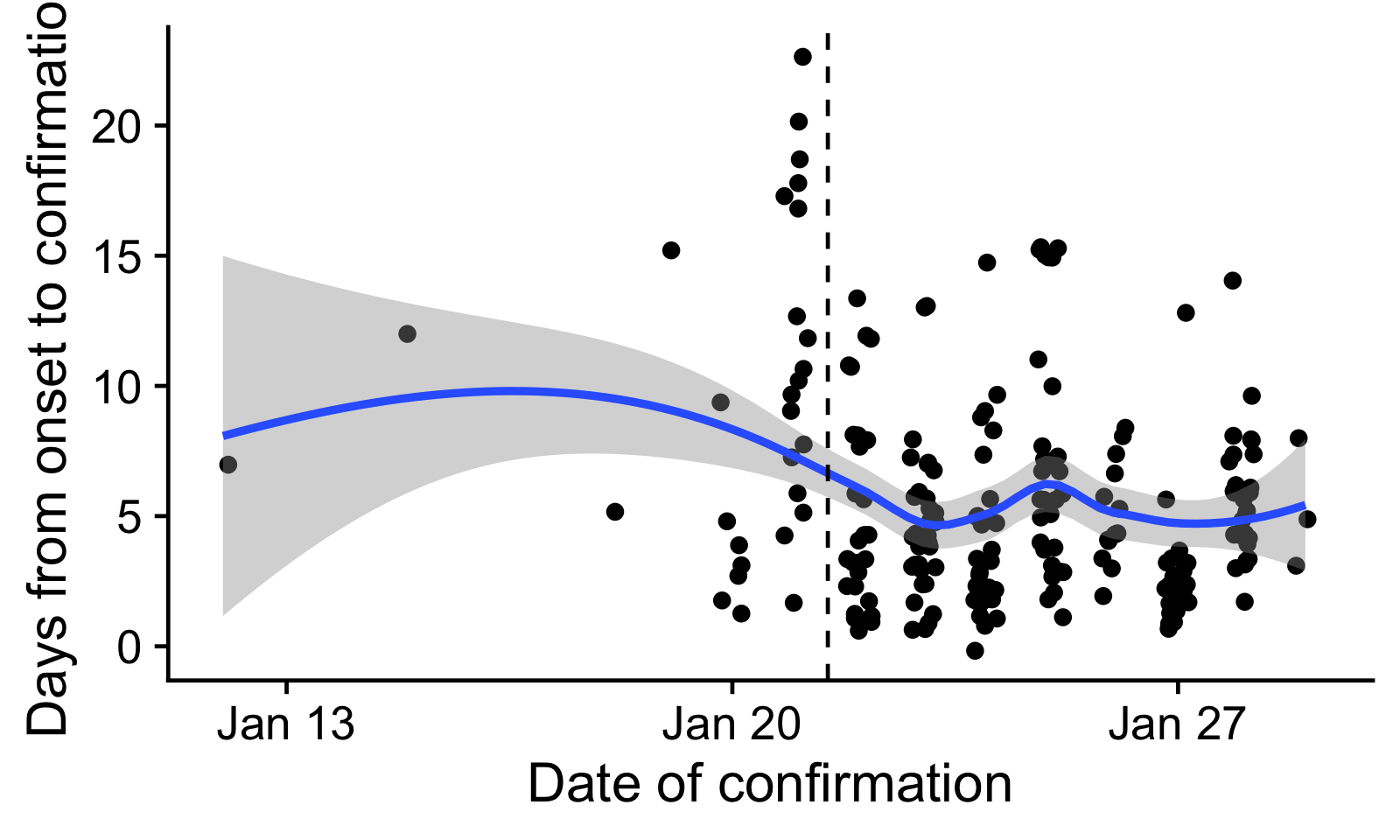
图像1: 出现症状到确诊的延迟时间。每一个点代表一例有报道症状和确诊时间到病例。蓝色的线是通过LOESS平滑法构建的趋势线。我们在进一步分析中仅使用了虚线右边的点。
根据发生症状到确诊的延迟时间计算确诊病例数量
症状出现后一天内的确诊率为10%、三天内为43%、5天内为64%。因此我们估计仍有大量积压病例将被确诊,但尚未报告。因此,请谨慎使用这些预测数据。如果在过去几天中症状到确诊的时间有所降低,我们将高估了实际案例数量。
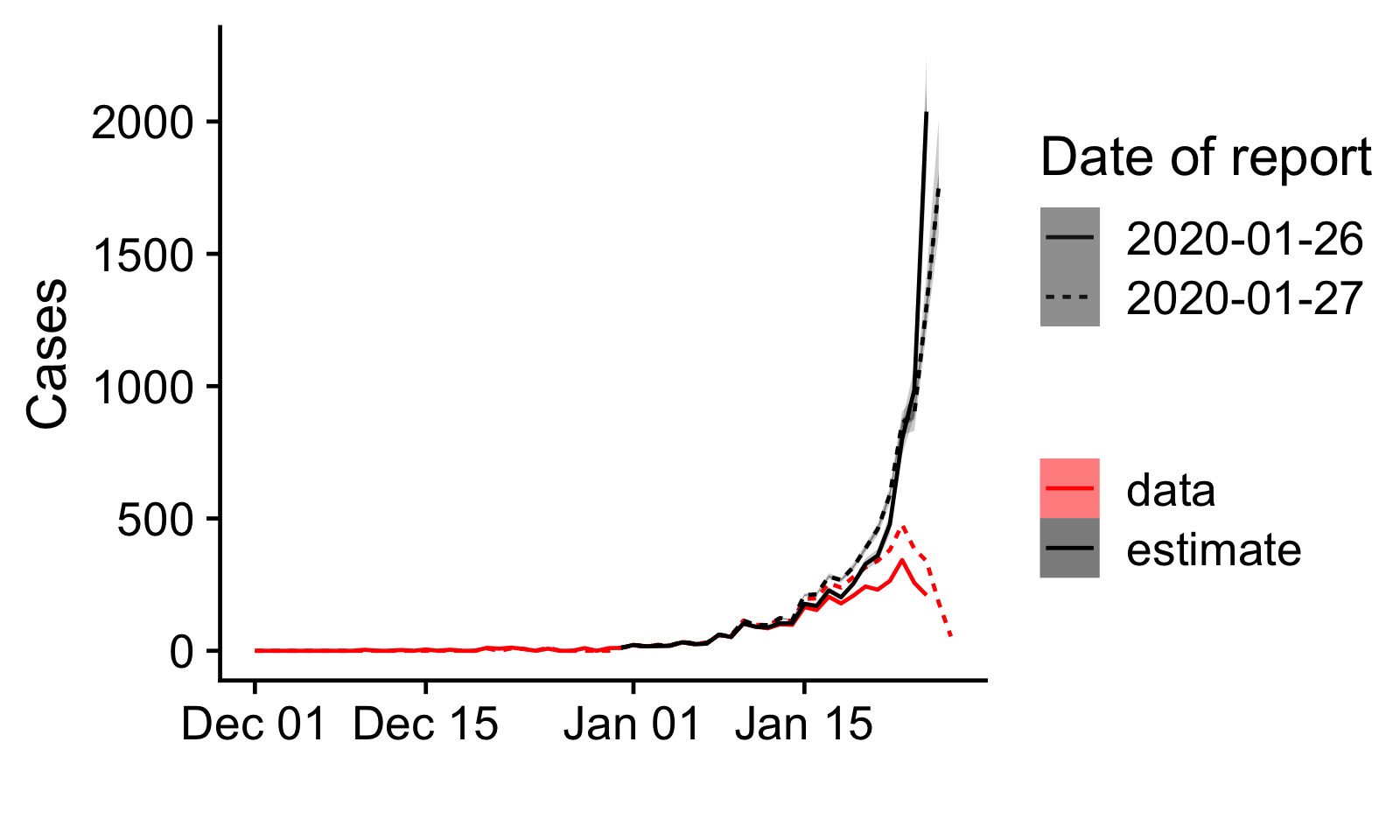
图像2;x轴为出现症状的时间,y轴为确诊病例数量。红色线代表的数据来自于中国疾病预防控制中心随后的两份报告。黑色为我们预测的确诊病例数量。X轴的日期为报告中案例的调查截止日期。
(随着时间变化的)再生数
再生数会随着时间变化。我们可以看到通过使用不同的连续病例间隔分布假设所产生的差异。根据早期流行病传播原理的连续时间病例分布,我们预计了基本传染数,发现没有明显下降趋势,但最近似乎有所上升。这可能是因为从发现症状到确诊的延迟时间变化了的原因,尤其是如果某些案例比我们预计的确诊时间更接近当前。
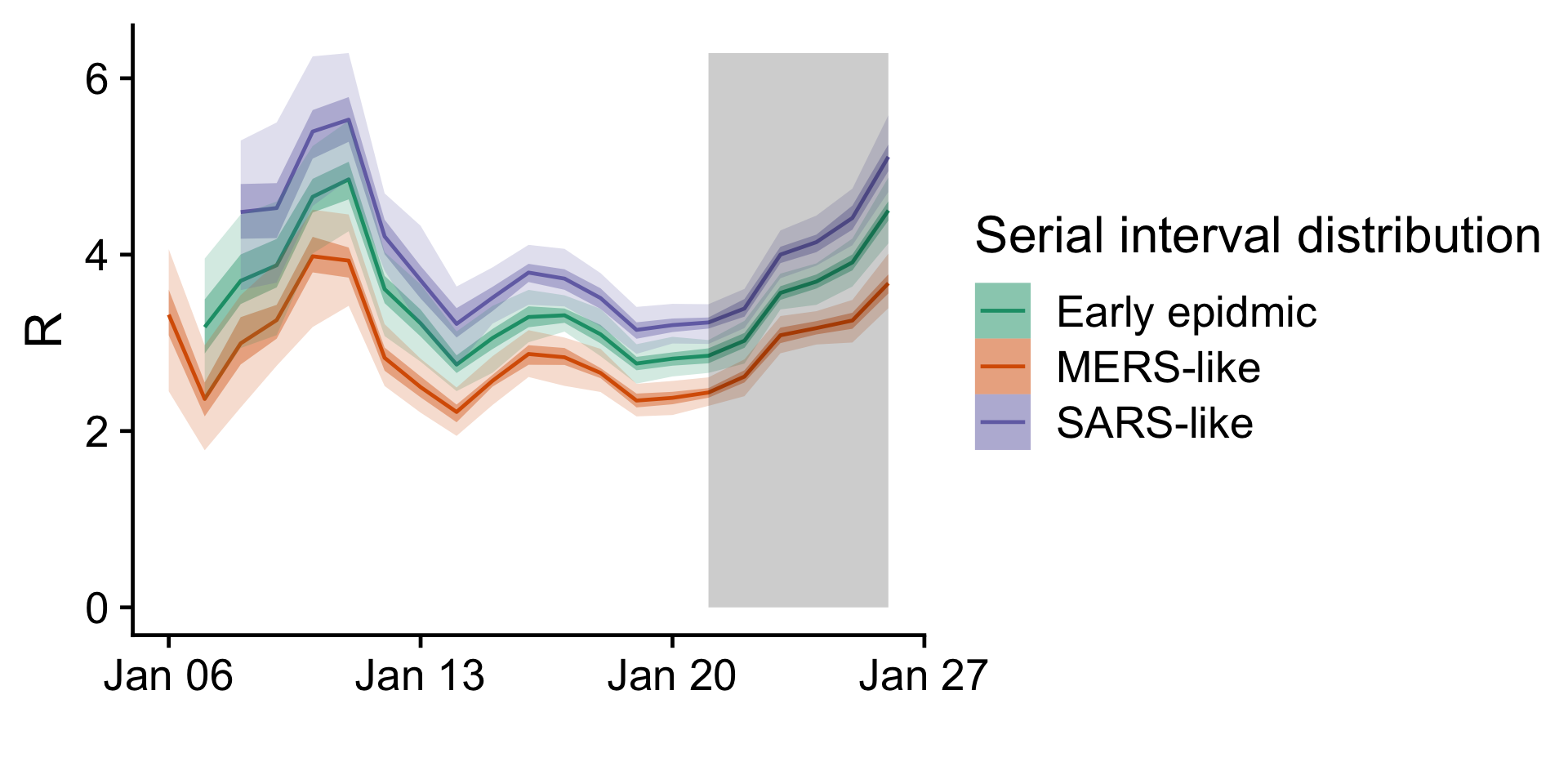
图像3:x轴为时间,y轴为根据不同连续病例时间分布预测的再生数。灰色阴影区间表示总预测案例超过实际预测案例50%的时间区间;这些区域有着非常高的不确定性。
参考文献
1 Xu B, Gutierrez B, Hill S et al. Epidemiological Data from the nCoV-2019 Outbreak: Early Descriptions from Publicly Available Data. 2020.
2 Cori A. EpiEstim: Estimate time varying reproduction numbers from epidemic curves. 2019. https://CRAN.R-project.org/package=EpiEstim
3 R Core Team. R: A language and environment for statistical computing. Vienna, Austria:: R Foundation for Statistical Computing
4 Cori A, Ferguson NM, Fraser C et al. A New Framework and Software to Estimate Time-Varying Reproduction Numbers During Epidemics. American Journal of Epidemiology 2013;178:1505–12. doi:10.1093/aje/kwt133
5 Wallinga J, Teunis P. Different Epidemic Curves for Severe Acute Respiratory Syndrome Reveal Similar Impacts of Control Measures. American Journal of Epidemiology 2004;160:509–16. doi:10.1093/aje/kwh255
6 Li Q, Guan X, Wu P et al. Early transmission dynamics in wuhan, china, of novel coronavirus–infected pneumonia. New England Journal of Medicine;0:null. doi:10.1056/NEJMoa2001316
7 Lipsitch M. Transmission Dynamics and Control of Severe Acute Respiratory Syndrome. Science 2003;300:1966–70.
8 Cauchemez S, Nouvellet P, Cori A et al. Unraveling the drivers of mers-cov transmission. Proceedings of the National Academy of Sciences 2016;113:9081–6. doi:10.1073/pnas.1519235113
9 Wu P, Hao X, Lau EHY et al. Real-time tentative assessment of the epidemiological characteristics of novel coronavirus infections in wuhan, china, as at 22 january 2020. Eurosurveillance 2020;25. doi:https://doi.org/10.2807/1560-7917.ES.2020.25.3.2000044
10 Epidemic update and risk assessment of 2019 novel coronavirus. 27 january, 2020. http://www.chinacdc.cn/jkzt/crb/zl/szkb_11803/jszl_11811/202001/P020200127544648420736.pdf
11 Epidemic update and risk assessment of 2019 novel coronavirus. 28 january, 2020. http://www.chinacdc.cn/yyrdgz/202001/P020200128523354919292.pdf