Projecting contact matrices in 177 geographical regions: an update and comparison with empirical data for the COVID-19 era

This study has not yet been peer reviewed.

You can read the full preprint here and the supplementary information here.

The risk of contracting a directly-transmitted infectious disease such as the Coronavirus Disease 2019 (COVID-19) depends on who interacts with whom. Such person-to-person interactions vary by age and locations—e.g., at home, at work, at school, or in the community—due to the different social structures. These social structures, and thus contact patterns, vary across and within countries. Although social contact patterns can be measured using contact surveys, the majority of countries around the world, particularly low- and middle-income countries, lack nationally-representative contact surveys. A simple way to present contact data is to use matrices where the elements represent the rate of contact between subgroups such as age groups represented by the columns and rows. In 2017, we generated age- and location-specific synthetic contact matrices for 152 geographical regions by adapting contact pattern data from eight European countries using country-specific data on household size, school and workplace composition. We have now updated these matrices with the most recent data (Demographic Household Surveys, World Bank, UN Population Division) extending the coverage to 177 geographical locations, covering 97.2% of the world’s population. We also quantified contact patterns in rural and urban settings. When compared to out-of-sample empirically-measured contact patterns, we found that the synthetic matrices reproduce the main features of these contact patterns. Figure 1: Comparison of the normalised empirical and synthetic age-specific contact matrices in ten geographical regions.The empirical matrices collected from contact surveys, modelled synthetic contact matrices, and the scatter plots of the entries in the observed (x-axis) and modelled (y-axis) contact matrices are presented. The correlation between the empirical and synthetic matrices are shown. The matrices are normalised such that its dominant eigenvalue is 1. To match the population surveyed in the empirical studies, the contact matrices from rural settings of Kenya, Peru, South Africa, Uganda, Vietnam, and Zimbabwe are presented; and the contact matrices from urban settings of China and the Russian Federation are presented. No data are available in the grey regions.

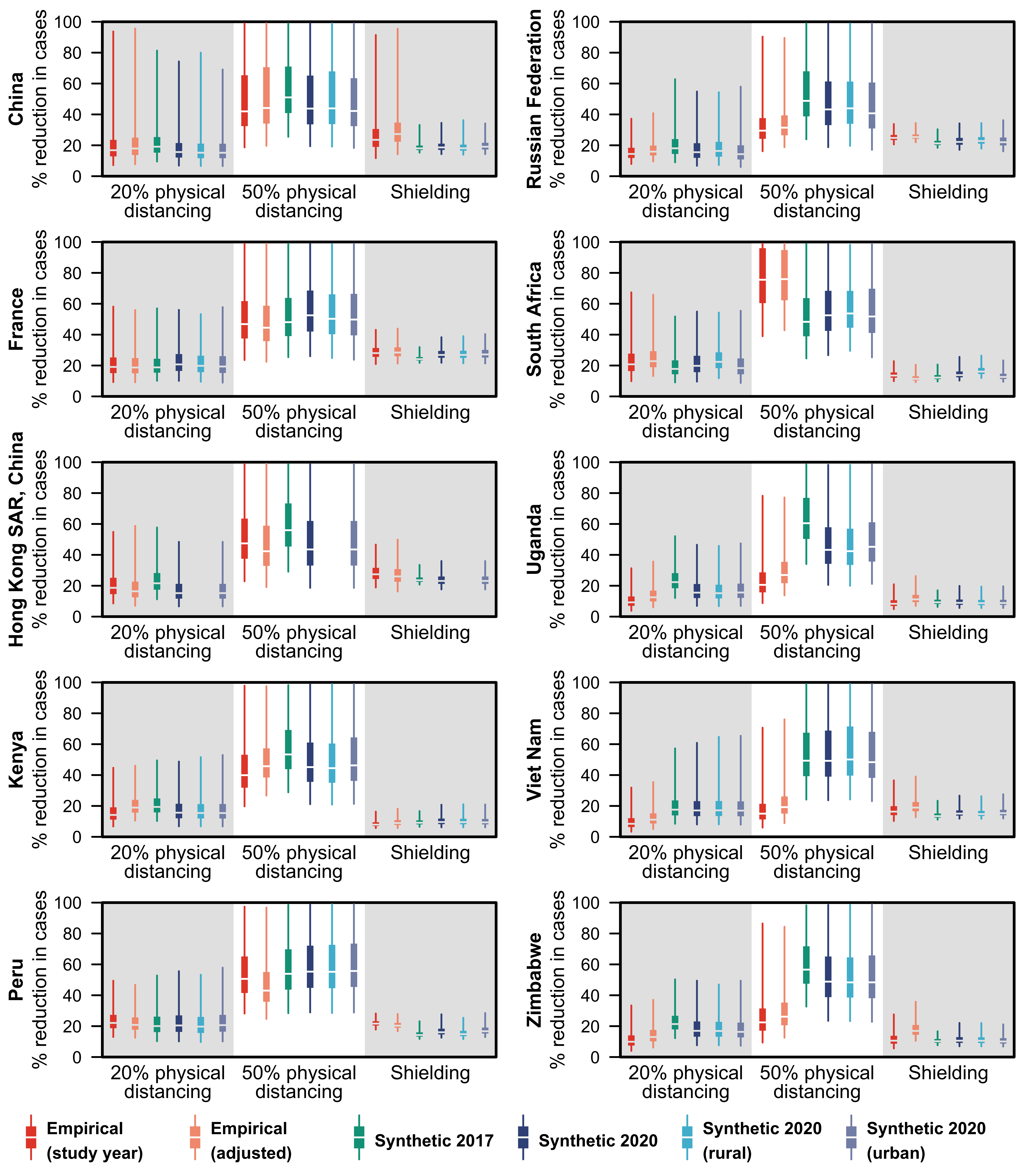Figure 4: Relative reduction in cases due to interventions in models of COVID-19 epidemics under three intervention scenarios in ten geographical regions using the empirical and synthetic matrices. The percentage reduction in cases in each of the three intervention scenario—20% physical distancing, 50% physical distancing, and shielding—against the unmitigated epidemic under different contact matrices is shown in the boxplots with boxes bounded by the interquartile range (25th and 75th percentiles), median in white and, whiskers spanning the2.5–97.5th percentiles. Six contact matrices were considered in the COVID-19 modelling: the empirically-constructed contact matrices at the study-year and adjusted for the 2020 population, the 2017 synthetic matrices, and the updated synthetic matrices at the national, rural, or urban settings.

Data availability: All data used in this study can be downloaded from the cited references. The codes used to generate these analyses and the updated synthetic matrices are available at Github.